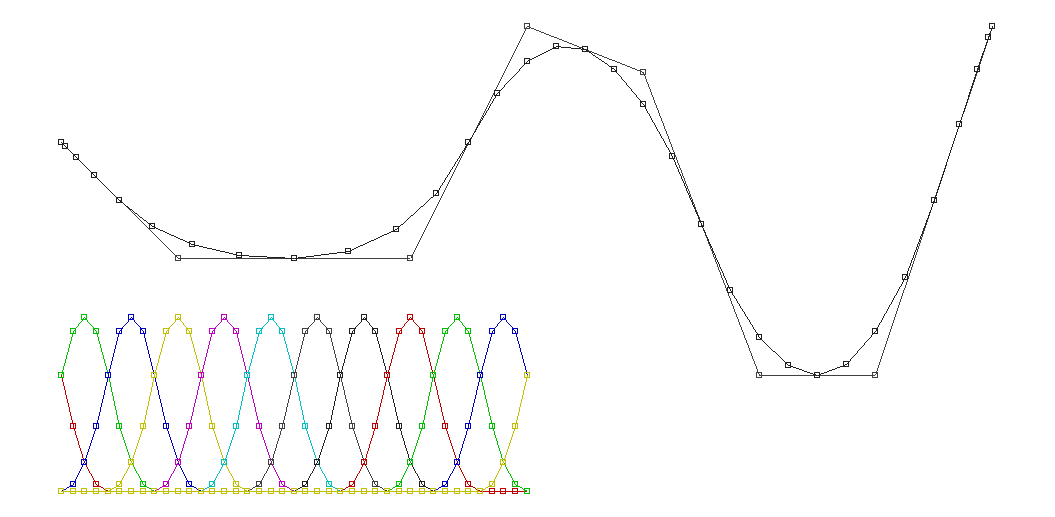
2 次 B スプライン https://ja.wikipedia.org/wiki/B-スプライン曲線 より 1/2 *t*t 1/2 * t*t ; bj,2(t) = -t*t + t+ 1/2 1/2 * (-2*t*t + 2*t + 1) 1/2 *(1-t)*(1-t) 1/2 * ( t*t - 2*t + 1) t : 0.0 0.0 0.5 0.5 t : 0.5 0.125 0.75 0.125 t : 1.0 0.5 0.5 0.0
3D グラフィックスのための数学入門 157 ページをコードに. コードは,kodatuno を参考にさせてもらった. double BS_basis (const double t,c_v_double& knot,const long order,const long i) { if (order <= 0) { return 0. ; } if (order == 1) { // Ni,0(t) if (t == knot[knot.size()-1]) { if (knot[i]<=t && t<=knot[i+1]) { return 1. ; } else { return 0. ; } } else { if (knot[i]<=t && t< knot[i+1]) { return 1. ; } else { return 0. ; } } } else { double n1 = 0 ; // (*/0) --> n = 0 double n2 = 0 ; double d1 = knot[i+order-1] - knot[i ] ; // T(i+k) -T(i) double d2 = knot[i+order-0] - knot[i+1] ; // T(i+k+1)-T(i+1) if (!::V1_is_near<double<(d1,0)) { n1 = t - knot[i] ; // t - T(i) n1 = n1 * BS_basis(t,knot,order-1,i ) ; // N(i, k-1)(t) n1 = n1 / d1 ; } if (!::V1_is_near<double<(d2,0)) { n2 = knot[i+order-0] - t ; // T(i+k+1)-t n2 = n2 * BS_basis(t,knot,order-1,i+1) ; // N(i+1,k-1)(t) n2 = n2 / d2 ; } return (n1 + n2) ; } return -1. ; } 同じページにある「簡略化計算公式」 double BS_basis (const double t,const long order,const long i) { if (order <= 0) { return 0. ; } if (order == 1) { // Ni,0(t) if (i<=t && t< i+1) { return 1. ; } else { return 0. ; } } else { double n1 = 0 ; double n2 = 0 ; double d1 = order - 1 ; // k double d2 = order - 1 ; // k if (!::V1_is_near<double<(d1,0)) { n1 = t - i ; // t-i n1 = n1 * BS_basis(t,order-1,i ) ; // N(i ,k-1) n1 = n1 / d1 ; } if (!::V1_is_near<double<(d2,0)) { n2 = (i+order-0) - t ; // i+k+1 - t n2 = n2 * BS_basis(t,order-1,i+1) ; // N(i+1,k-1) n2 = n2 / d2 ; } return (n1 + n2) ; } return -1. ; }
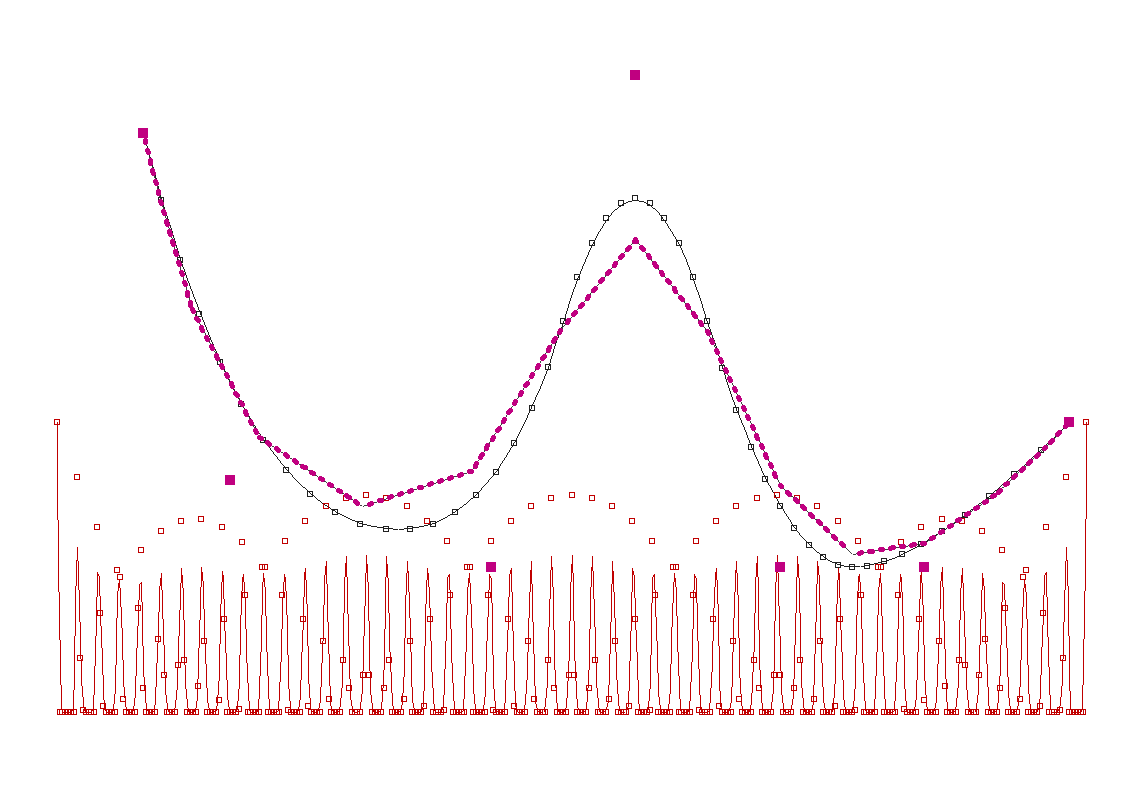
次の様なコードでよく見る画像に.画像は重ね合せている.ループの部分がスマートでない. long pt_count = 7 ; v_vd_n.resize(pt_count) ; for (size_t index=0 ; index<10 ; index++) { for (size_t index_d=0 ; index_d<div_c ; index_d++) { double t = double(index*div_c + index_d)/div_c ; for (size_t i=0 ; i<pt_count ; i++) { double r = ::BS_basis(t,order,i) ; Vd3A v3a = v_vd_n[i] ; Vd3 v(v3a.size(),r*100,0) ; v3a.push_back(v) ; v_vd_n[i] = v3a ; } } }
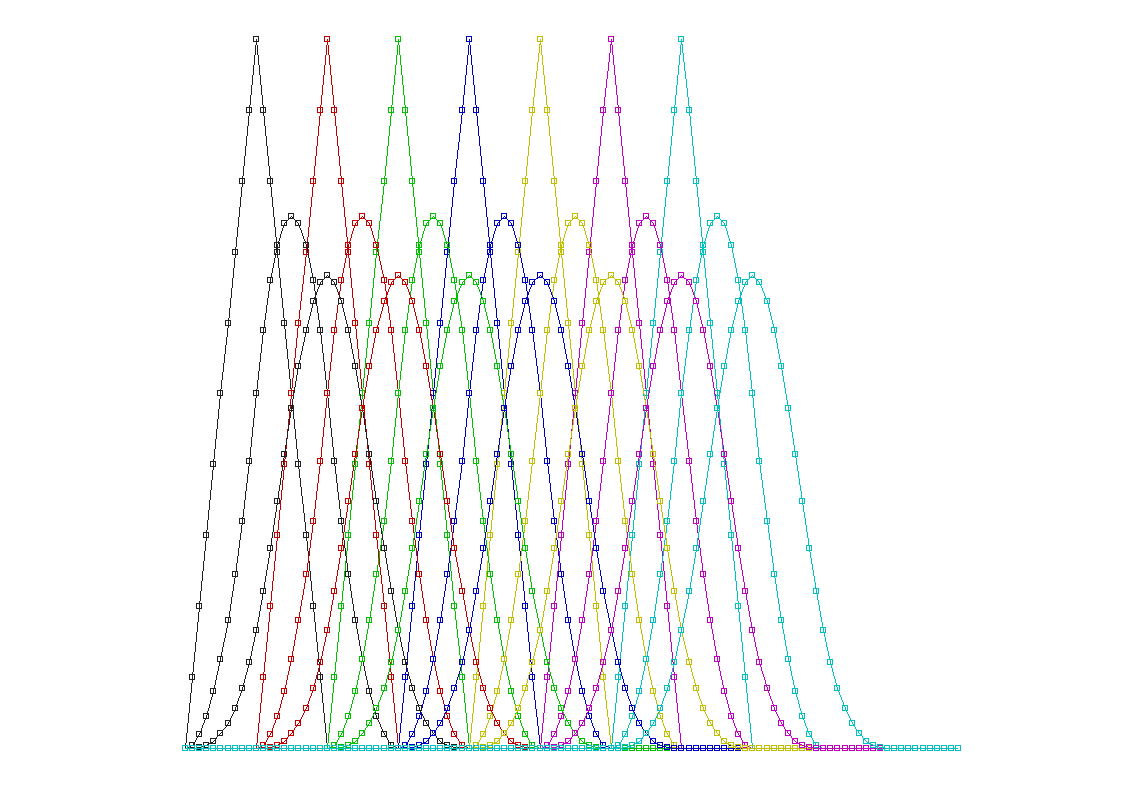
3 次,4 分割 size_t order = 4 ; size_t degree = order - 1 ; double div_c = 10. ; div_c = 4. ; v_vd_n.resize(pt.size()) ; for (double j=degree * div_c ; j<=pt.size()*div_c ; j++) { double t = j/div_c ; double x = 0 ; double y = 0 ; for (size_t i=0 ; i<pt.size() ; i++) { double r = BS_basis(t,order,i) ; x += pt[i].x * r ; y += pt[i].y * r ; { size_t vi = i ; Vd3A v3a = v_vd_n[vi] ; Vd3 v(v3a.size()*5,r*100,0) ; v3a.push_back(v) ; v_vd_n[vi] = v3a ; } } Vd3 spt(x,y,0) ; sp.push_back(spt) ; }

2 次,2 分割
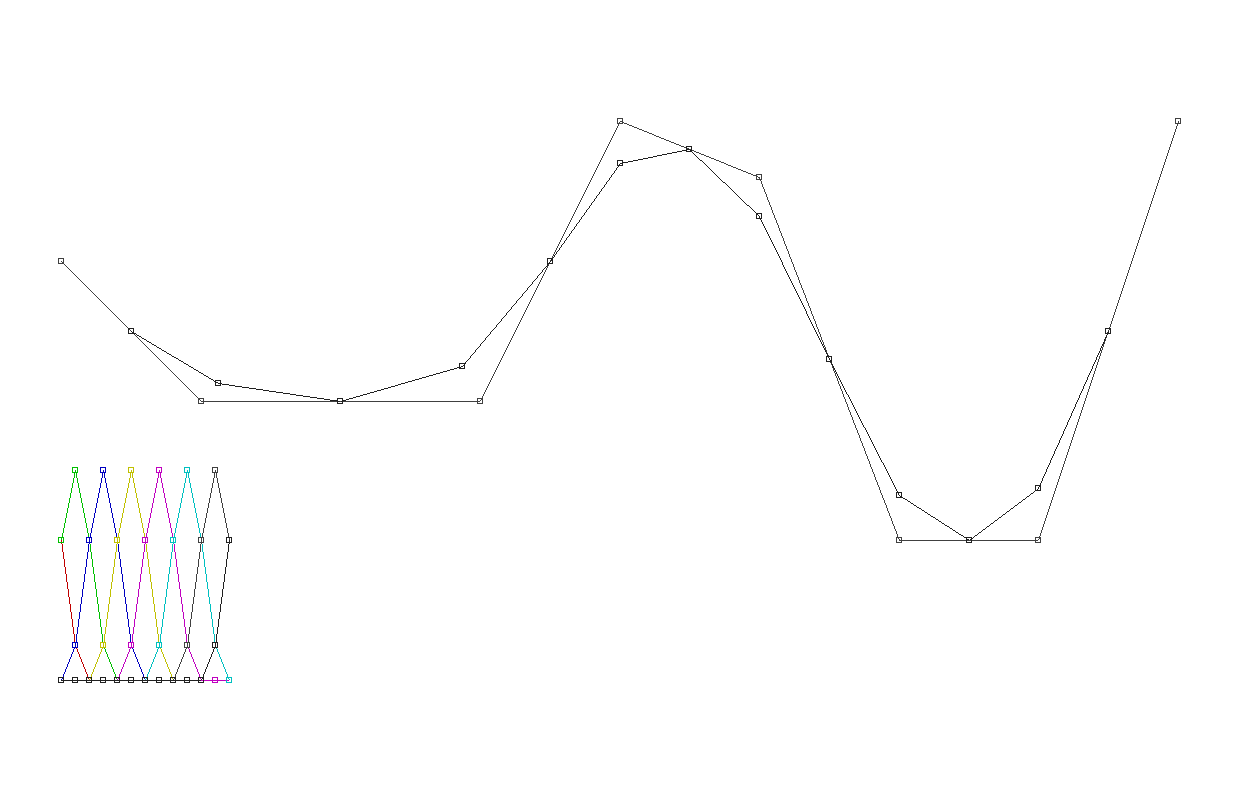
最初と最後の点を繰り返し