
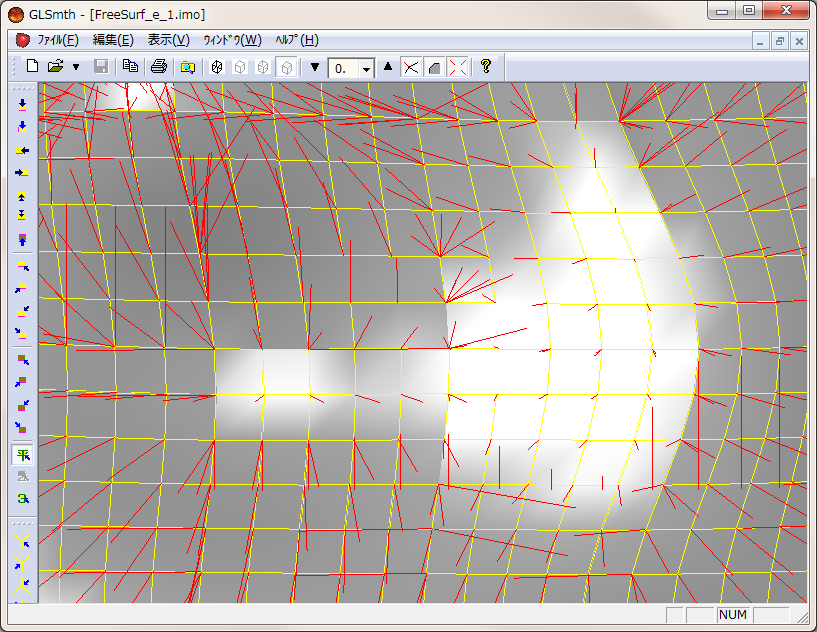
Kodatuno にあるサンプルを少し編集したデータ 与えられた頂点を単純に結んで面に. FreeSurf_e_0.html 単純に結んで四角形にして,さらに平均の位置から 4 つの三角形に分割している. B-Spline で表示すると, FreeSurf_e_1.html inp ファイルで与えている制御点の付近が滑らかでない.
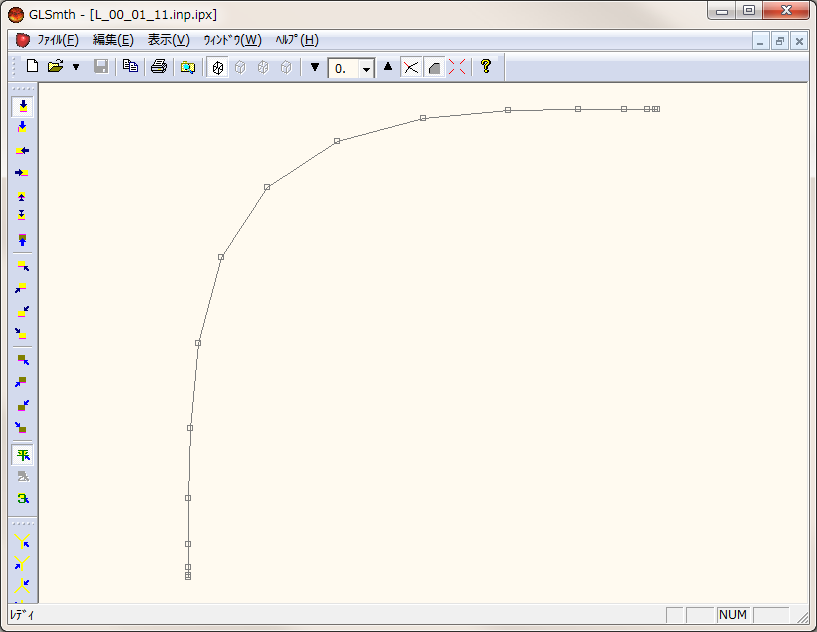
 次の様な 3 点を与えて,曲線に.
L_00_01_11.inp
0,0,0
0,10,0
10,10,0
次の様な 3 点を与えて,曲線に.
L_00_01_11.inp
0,0,0
0,10,0
10,10,0
 見た目はわからないが,そのデータを見ると頂点が連続している部分がある(頂点番号の 4,8,12).
1 1 ; PartsA Exporter Ver.1.20 2015/06/18 "c:\Temp\Test_3D\Read_3D\Debug.060\Read_3D.exe"
8355711 0 "" "'0' '0.3' '8355711' '1.5' '1.5' " "'1' '16777215' '11' " "'0.2' '0' '2.5' "
80 "0 0 1 " "0 0 0 " "10 10 0 " "1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 " 0 0
17 1 ; P3A_
0 0 0
0 0.026041666666667 0
0 0.208333333333333 0
0 0.703125 0
0 1.66666666666667 0
0.026041666666667 3.17708333333333 0
0.208333333333333 5 0
0.703125 6.82291666666667 0
1.66666666666667 8.33333333333333 0
3.17708333333333 9.296875 0
5 9.79166666666667 0
6.82291666666667 9.97395833333333 0
8.33333333333333 10 0
9.296875 10 0
9.79166666666667 10 0
9.97395833333333 10 0
10 10 0
0 1 ; TextA
0 1 ; LineA
0 1 ; CircleA
1 1 ; FaceA
20 20 20 "0 1 2 3 4 4 5 6 7 8 8 9 10 11 12 12 13 14 15 16 " "-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 " 0 -1
0 1 ; FaceA ; * * *
0 1 ; FaceA
0 1 ; EdgeA
0 1 ; PointA
0 1 ; TextA
0 1 ; TextHA
0 1 ; TextVA
0 1 ; PointA
連続する部分をスキップする様に変更
inline Vd3A b_spline (const Vd3A& pnts,const long div_n=2)
{
Vd3A vd3a ;
if (pnts.size() < 3) { return pnts ; }
if (pnts.size()== 3) {
Vd3A v_pnt ;
v_pnt.push_back(pnts[0]) ;
v_pnt.push_back(pnts[0]) ;
v_pnt.push_back(pnts[1]) ;
v_pnt.push_back(pnts[2]) ;
v_pnt.push_back(pnts[2]) ;
vd3a = ::b_spline(v_pnt,div_n) ;
}
else { // 3 <
{ // 0,1,2
{
Vd3 p0 = pnts[0] ;
Vd3 p1 = pnts[0] ;
Vd3 p2 = pnts[1] ;
Vd3 p3 = pnts[2] ;
{ // is close ?
Vd3 p_0 = pnts[0] ;
Vd3 p_l = pnts[pnts.size()-1] ;
if (p_0 == p_l) {
p0 = pnts[pnts.size()-2] ;
}
}
Vd3A vd_0 = ::b_spline(p0,p1,p2,p3,div_n) ;
vd3a.insert(vd3a.end(),vd_0.begin(),vd_0.end()) ;
}
}
{ // 1 - (n-2)
for (size_t index=3 ; index<pnts.size() ; index++) {
Vd3 p0 = pnts[index-3] ;
Vd3 p1 = pnts[index-2] ;
Vd3 p2 = pnts[index-1] ;
Vd3 p3 = pnts[index-0] ;
Vd3A vd__ = ::b_spline(p0,p1,p2,p3,div_n) ;
if (vd3a.size()>0 && vd__.size()>0) {
Vd3 pl = vd3a[vd3a.size()-1] ;
Vd3 pn = vd__[0] ;
if (::V3_is_near(pl,pn)) {
vd3a.pop_back() ;
}
}
vd3a.insert(vd3a.end(),vd__.begin(),vd__.end()) ;
}
}
{ // n-3,n-2,n-1
{
Vd3 p0 = pnts[pnts.size()-3] ;
Vd3 p1 = pnts[pnts.size()-2] ;
Vd3 p2 = pnts[pnts.size()-1] ;
Vd3 p3 = pnts[pnts.size()-1] ;
{ // is close ?
Vd3 p_0 = pnts[0] ;
Vd3 p_l = pnts[pnts.size()-1] ;
if (p_0 == p_l) {
p3 = pnts[1] ;
}
}
Vd3A vd_l = ::b_spline(p0,p1,p2,p3,div_n) ;
if (vd3a.size()>0 && vd_l.size()>0) {
Vd3 pl = vd3a[vd3a.size()-1] ;
Vd3 pn = vd_l[0] ;
if (::V3_is_near(pl,pn)) {
vd3a.pop_back() ;
}
}
vd3a.insert(vd3a.end(),vd_l.begin(),vd_l.end()) ;
}
}
}
return vd3a ;
}
FreeSurf_e_2.html
見た目はわからないが,そのデータを見ると頂点が連続している部分がある(頂点番号の 4,8,12).
1 1 ; PartsA Exporter Ver.1.20 2015/06/18 "c:\Temp\Test_3D\Read_3D\Debug.060\Read_3D.exe"
8355711 0 "" "'0' '0.3' '8355711' '1.5' '1.5' " "'1' '16777215' '11' " "'0.2' '0' '2.5' "
80 "0 0 1 " "0 0 0 " "10 10 0 " "1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 " 0 0
17 1 ; P3A_
0 0 0
0 0.026041666666667 0
0 0.208333333333333 0
0 0.703125 0
0 1.66666666666667 0
0.026041666666667 3.17708333333333 0
0.208333333333333 5 0
0.703125 6.82291666666667 0
1.66666666666667 8.33333333333333 0
3.17708333333333 9.296875 0
5 9.79166666666667 0
6.82291666666667 9.97395833333333 0
8.33333333333333 10 0
9.296875 10 0
9.79166666666667 10 0
9.97395833333333 10 0
10 10 0
0 1 ; TextA
0 1 ; LineA
0 1 ; CircleA
1 1 ; FaceA
20 20 20 "0 1 2 3 4 4 5 6 7 8 8 9 10 11 12 12 13 14 15 16 " "-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 " 0 -1
0 1 ; FaceA ; * * *
0 1 ; FaceA
0 1 ; EdgeA
0 1 ; PointA
0 1 ; TextA
0 1 ; TextHA
0 1 ; TextVA
0 1 ; PointA
連続する部分をスキップする様に変更
inline Vd3A b_spline (const Vd3A& pnts,const long div_n=2)
{
Vd3A vd3a ;
if (pnts.size() < 3) { return pnts ; }
if (pnts.size()== 3) {
Vd3A v_pnt ;
v_pnt.push_back(pnts[0]) ;
v_pnt.push_back(pnts[0]) ;
v_pnt.push_back(pnts[1]) ;
v_pnt.push_back(pnts[2]) ;
v_pnt.push_back(pnts[2]) ;
vd3a = ::b_spline(v_pnt,div_n) ;
}
else { // 3 <
{ // 0,1,2
{
Vd3 p0 = pnts[0] ;
Vd3 p1 = pnts[0] ;
Vd3 p2 = pnts[1] ;
Vd3 p3 = pnts[2] ;
{ // is close ?
Vd3 p_0 = pnts[0] ;
Vd3 p_l = pnts[pnts.size()-1] ;
if (p_0 == p_l) {
p0 = pnts[pnts.size()-2] ;
}
}
Vd3A vd_0 = ::b_spline(p0,p1,p2,p3,div_n) ;
vd3a.insert(vd3a.end(),vd_0.begin(),vd_0.end()) ;
}
}
{ // 1 - (n-2)
for (size_t index=3 ; index<pnts.size() ; index++) {
Vd3 p0 = pnts[index-3] ;
Vd3 p1 = pnts[index-2] ;
Vd3 p2 = pnts[index-1] ;
Vd3 p3 = pnts[index-0] ;
Vd3A vd__ = ::b_spline(p0,p1,p2,p3,div_n) ;
if (vd3a.size()>0 && vd__.size()>0) {
Vd3 pl = vd3a[vd3a.size()-1] ;
Vd3 pn = vd__[0] ;
if (::V3_is_near(pl,pn)) {
vd3a.pop_back() ;
}
}
vd3a.insert(vd3a.end(),vd__.begin(),vd__.end()) ;
}
}
{ // n-3,n-2,n-1
{
Vd3 p0 = pnts[pnts.size()-3] ;
Vd3 p1 = pnts[pnts.size()-2] ;
Vd3 p2 = pnts[pnts.size()-1] ;
Vd3 p3 = pnts[pnts.size()-1] ;
{ // is close ?
Vd3 p_0 = pnts[0] ;
Vd3 p_l = pnts[pnts.size()-1] ;
if (p_0 == p_l) {
p3 = pnts[1] ;
}
}
Vd3A vd_l = ::b_spline(p0,p1,p2,p3,div_n) ;
if (vd3a.size()>0 && vd_l.size()>0) {
Vd3 pl = vd3a[vd3a.size()-1] ;
Vd3 pn = vd_l[0] ;
if (::V3_is_near(pl,pn)) {
vd3a.pop_back() ;
}
}
vd3a.insert(vd3a.end(),vd_l.begin(),vd_l.end()) ;
}
}
}
return vd3a ;
}
FreeSurf_e_2.html
